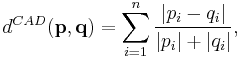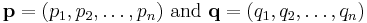Canberra distance
The Canberra distance is a numerical measure of the distance between pairs of points in a vector space, introduced in 1966[1] and refined in 1967[2] by G. N. Lance and W. T. Williams. It is similar to the Manhattan distance. It is mostly used for data scattered around the origin.
Contents |
Formal description
The Canberra distance, 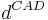 , between two vectors
, between two vectors 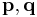 in an n-dimensional real vector space is given as follows:
in an n-dimensional real vector space is given as follows:
where
are vectors.
See also
Notes
- ^ Lance, G. N.; Williams, W. T. (1966). "Computer programs for hierarchical polythetic classification ("similarity analysis").". Computer Journal 9 (1): 60–64. doi:10.1093/comjnl/9.1.60.
- ^ Lance, G. N.; Williams, W. T. (1967). "Mixed-data classificatory programs I.) Agglomerative Systems". Australian Computer Journal: 15–20.
References
- Schulz, Jan. "Canberra distance". Code 10. http://www.code10.info/index.php?option=com_content&view=article&id=49:article_canberra-distance&catid=38:cat_coding_algorithms_data-similarity&Itemid=57. Retrieved 18 October 2011.